The Monty Hall Problem – Easy Hacks for Solving It

When it’s the time to think logically we usually can’t handle our cool even if the car of our dreams is at stake. Such is the case with the Monty Hall problem. It turns out that even if we had the opportunity of a lifetime we would still blow it due to a mind clouded by irrational thoughts. Good thing, “rational” is our middle name.

This problem has been plaguing the intellectual fraternity for years now leaving us little choice but to introduce you to the dilemma itself and how we prefer to approach it. You might want to lend an ear to what we have to say about problem-solving and how to behave in an unnerving situation when the dreaded reality of leaving empty-handed is ever so present. We’ve run across many brilliant solutions to the Monty Hall paradox, which are sure to give an idea of how to best tackle it.

The Monty Hall Problem Simulation

The Monty Hall problem was named after the host of the American TV show Let’s Make a Deal. Monty Hall was one of the biggest entertainers known to the American public and he was known for dishing out unseemly sums of money to the audience. But what this easily amiable man was famed for is this puzzling game of his where only one of three doors lead to a brand-new car and the other two are practically baits. Monty would let you name a number between one and three and then kindly saying out loud a number of his own, only to reveal one of the zonks.

Left with only two doors, the host then asks if you’d like to switch. At this moment all kinds of intrusive thoughts start creeping in to dissuade you from changing your decision. Make it or break it call, is there something you can make other than hoping to cop it sweet or you are doomed to fail miserably when asked what’s next? As it stands this dilemma has become the hotspot for endless debates that have been going on for years.

The popular opinion is that the chance of taking home the shiny car is either 50% or 66%. In the end, everyone comes down on one side or the other. What’s the bone of contention and how not to fall for the deceiving words of the host but stay true to logic? We’ll dismantle the problem piece by piece and show you what’s the right thing to do given the circumstances.

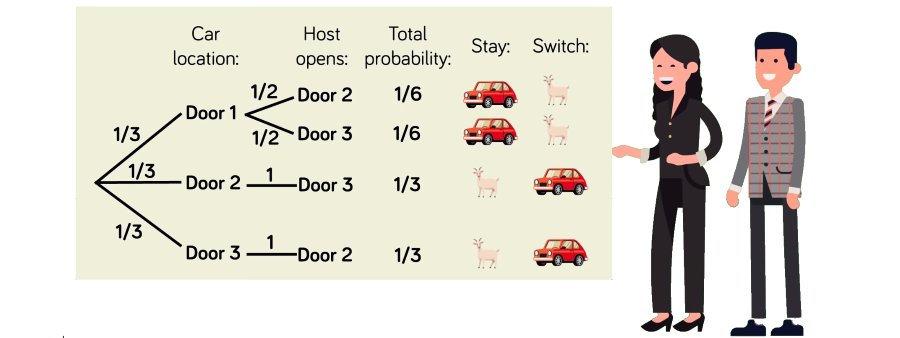
Monty Hall Explained the Best

Why switch? There’s no better way to exemplify why switching is a good idea than starting with the obvious question – which is more likely to happen when you’re facing all three doors, to pick a goat or the car? Obviously, you’ll land on a goat every two out of three tries when choosing between three different options. Looking at it in this way, switching after one of the two goats is revealed will result in claiming the car in 66% of the time. The suggestion that you will rather lose the car by switching assumes that you’ve picked the correct door, to begin with when all three of them were closed, which could be true only 33% of the time. Maybe it won’t yet jump out at you why that is, but hold fast we’ve included a few more solutions to clarify on the point made.

1/3 vs 2/3 Where’s the Catch?

The essence of the problem is within the rest of the doors we are not choosing. There’s a 2/3 chance the big prize is behind one of them but in the beginning, we still don’t have a clue where could any of the two goats be. That changes the moment the host opens one of the other two doors and reveals goat number one. Do you like those “two at the price of one” kind of deals? That’s exactly what happens here. We had two doors, which we can’t choose, representing 66% percent chance of success and now one of them is eliminated. Then why shouldn’t you switch to the remaining of the two doors? We’d do that, with bells on! There’s no logical reason not to accept the offer.

Vos Savant’s Take on the Dilemma

Vos Savant knew that most people struggle to picture the mathematical dynamic taking place when Monty cracks one of the doors open. That’s why she suggested a clearer example, revealing unambiguously what it means to be facing two doors instead of three. So, let’s look at the paradox from another angle, this time not with three but hundred doors.

To select the prize-winning door is a near impossible feat, but you go ahead and choose a number, maybe 55 because it looks cool. Other than a speed limitation, that number tells us very little about what could be hiding behind that door. In all honesty, a 1 in 100 chance-pick is a shot in a dark because we don’t have any information whatsoever about where the car would be.

Not until the host slams 98 doors wide open to show us all zonks except for one, that could be hiding in either of the two remaining doors. Now, we all know that we almost surely failed the first pick and then the host leaves us with only two numbers out of the initial 100. At this point, it should be abundantly clear that you should gladly make the switch if the car is behind one of the two doors. The remaining door must be the winning one since the host would never reveal the car.

What You’re Probably Still Missing

This is what we like to call the human factor. Wasn’t it for the duplicitous speech of the host, how your choice is revelational and you surely have got the jackpot in the bag you would probably switch intuitively. Sadly, the choice everyone does initially has nothing to do with the supernatural and who knows why people tend to stick with their gut instead of letting mathematics do its “magic”. Most players let themselves be talked into making the wrong decision, out of paranoia or for fear of looking stupid on TV, who knows exactly why.

For the most part, participants remain unaware of the other side of the equation, which is the host. That’s why they are easily tricked into thinking that even as is, with two doors, the chance of getting it right is 50% and switching won’t make much of a difference. But as it turns out, this is not exactly the case. The fact that the host knows where the car is, changes everything. Would he randomly opened one door leaving only two still closed, then it would be 50:50 picking the correct one. When we know that he is purposefully revealing a goat then we realize that switching cranks up the chance of success to 66%.

Wrapping it Up

We think this dive in probability theory and reverse psychology was quite educational for everyone. Remember that your best advisor is unbiased reasoning through analytical thinking, as Sherlock Holmes calls it – the art of deduction. This so obvious, yet not that easy to adopt approach can do miracles in the standard games of chance and this was the whole point of getting our hands dirty with Monty’s problem.

There’s no easy way around it, only precise calculations and careful assessment can get you out of a sticky situation. However, not everything goes by the book and occasionally you’ll get the short end of the stick. But that’s all in a day’s work for regular gamblers. The important thing is to follow a coherent course of action and make the most out of the given opportunity.